Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цель урока:
- обучающая – ввести понятие трапеции, познакомиться с видами трапеций, изучить свойства трапеции, научить учащихся применять полученные знания в процессе решения задач;
- развивающая – развитие коммуникативных качеств учащихся, развитие умения проводить эксперимент, обобщать, делать выводы, развитие интереса к предмету.
- воспитательная – воспитывать внимание, создать ситуацию успеха, радости от самостоятельного преодоления трудностей, развить у учащихся потребность в самовыражении через различные виды работ.
Формы работы: фронтальная, парная, групповая.
Форма организации деятельности детей: умение слушать, строить обсуждение, высказывать мысль, вопрос, дополнение.
Оборудование: компьютер, мультимедийный проектор, экран. На ученических столах: разрезной материал для составления трапеции у каждого ученика на парте; карточки с заданиями (распечатки чертежей и заданий из конспекта урока).
ХОД УРОКА
I. Организационный момент
Приветствие, проверка готовности рабочего места к уроку.
II. Актуализация знаний
- развитие умений классифицировать объекты;
- выделение главных и второстепенных признаков при классификации.
Рассматривается рисунок №1.

Далее идёт обсуждение рисунка.
– Из чего составлена данная геометрическая
фигура? Ответ ребята находят на рисунках: [из
прямоугольника и треугольников].
– Какими должны быть треугольники, составляющие
трапецию?
Выслушиваются и обсуждаются все мнения,
выбирается один вариант: [треугольники должны
быть обязательно прямоугольными].
– Как составляются треугольники и
прямоугольник? [Так, чтобы противоположные
стороны прямоугольника совпадали с катетом
каждого из треугольников].
– А что вы знаете о противоположных сторонах
прямоугольника? [Они параллельны].
– Значит, и в данном четырёхугольнике будут
параллельные стороны? [Да].
– Сколько их? [Две].
После обсуждения учитель демонстрирует
«королеву урока» - трапецию.
III. Объяснение нового материала
1. Определение трапеции, элементы трапеции
- научить учащихся давать определение трапеции;
- называть ее элементы;
- развитие ассоциативной памяти.
– А теперь попробуйте дать полное определение
трапеции. Каждый учащийся продумывает ответ на
вопрос. Обмениваются мнениями в паре, готовят
единый ответ на вопрос. Устный ответ дают по
одному учащемуся от 2-3 пар.
[Трапецией называется четырёхугольник, у
которого две стороны параллельны, а две другие
стороны не параллельны].
– Как называются стороны трапеции? [Параллельные стороны называются основаниями трапеции, а две другие – боковыми сторонами].
Учитель предлагает сложить из разрезных фигур трапеции. Учащиеся работают в парах, складывают фигуры. Хорошо, если пары учащихся будут разноуровневыми, тогда один из учеников является консультантом и помогает товарищу в случае затруднения.
– Постройте в тетрадях трапецию, запишите названия сторон трапеции. Задайте вопросы по чертежу своему соседу, выслушайте его ответы, сообщите свои варианты ответов.
Историческая справка
«Трапеция»
– слово греческое,
означавшее в древности «столик» (по гречески
«трапедзион» означает столик, обеденный стол.
Геометрическая фигура была названа так по
внешнему сходству с маленьким столом.
В «Началах» (греч. Στοιχεῖα, лат. Elementa) - главный труд
Евклида, написанный около 300 г. до н. э. и
посвящённый систематическому построению
геометрии) термин «трапеция» применяется не в
современном, а в другом смысле: любой
четырехугольник (не параллелограмм). «Трапеция»
в нашем смысле встречаются впервые у
древнегреческого математика Посидония (Iв.). В
средние века трапецией называли, по Евклиду,
любой четырехугольник (не параллелограмм); лишь в
XVIIIв. это слово приобретает современный смысл.
Построение трапеции по её заданным элементам. Ребята выполняют задания на карточке №1.

Учащимся приходится конструировать трапеции
самых разных расположений и начертаний. В пункте
1 необходимо построить прямоугольную трапецию. В
пункте 2 появляется возможность построить
равнобедренную трапецию. В пункте 3 трапеция
окажется «лежащей на боку». В пункте 4 рисунок
предусматривают построение такой трапеции, у
которой одно из оснований оказывается
непривычно маленьким.
Ученики «удивляют» учителя разными фигурами,
носящими одно общее название – трапеция. Учитель
демонстрирует возможные варианты построения
трапеций.
Задача 1
. Будут ли равны две трапеции, у
которых соответственно равны одно из оснований и
две боковые стороны?
Обсуждают решение задачи в группах, доказывают
правильность рассуждения.
По одному ученику от группы выполняет чертёж на
доске, объясняет ход рассуждений.
2. Виды трапеции
- развитие двигательной памяти, умений разбивать трапецию на известные фигуры, необходимые для решения задач;
- развитие умений обобщать, сравнивать, давать определение по аналогии, выдвигать гипотезы.
Рассмотрим рисунок:
– Чем отличаются трапеции, изображённые на
рисунке?
Ребята заметили, что вид трапеции зависит от вида
треугольника, расположенного слева.
– Дополните предложение:
Трапеция называется прямоугольной, если …
Трапеция называется равнобедренной, если …

3. Свойства трапеции. Свойства равнобедренной трапеции.
- выдвижение по аналогии с равнобедренным треугольником гипотезы о свойстве равнобедренной трапеции;
- развитие аналитических умений (сравнивать, выдвигать гипотезу, доказывать, строить).
- Отрезок, соединяющий середины диагоналей, равен полуразности оснований.
- У равнобедренной трапеции углы при любом основании равны.
- У равнобедренной трапеции диагонали равны.
- У равнобедренной трапеции высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой – полуразности оснований.
Задача 2.
Докажите, что в
равнобедренной трапеции: а) углы при каждом
основании равны; б) диагонали равны. Для
доказательства этих свойств равнобедренной
трапеции вспоминаются признаки равенства
треугольников. Учащиеся выполняют задание в
группах, обсуждают, записывают решение в тетради.
По одному ученику от группы проводят
доказательство у доски.
4. Упражнение на внимание
5. Примеры применения форм трапеций в повседневной жизни:
- в интерьерах (диваны, стены, навесные потолки);
- в ландшафтном дизайне (границы газонов, искусственных водоемов, камней);
- в индустрии моды (одежда, обувь, аксессуары);
- в дизайне предметов повседневного пользования (светильники, посуда, с использованием форм трапеции);
- в архитектуре.
Практическая работа (по вариантам).
– В одной системе координат постройте равнобедренные трапеции по заданным трём вершинам.
1 вариант: (0; 1), (0; 6), (– 4; 2), (…; …) и (– 6; – 5), (4; – 5),
(– 4; – 3), (…; …).
2 вариант: (– 1; 0), (4; 0), (6; 5), (…; …) и (1; – 2), (4; – 3), (4;
– 7), (…; …).
– Определите координаты четвёртой вершины.
Решение проверяется и комментируется всем
классом. Учащиеся указывают координаты
четвёртой найденной точки и устно пытаются
объяснить, почему заданные условия определяют
только одну точку.
Занимательная задача. Сложить трапецию из: а) четырёх прямоугольных треугольников; б) из трёх прямоугольных треугольников; в) из двух прямоугольных треугольников.
IV. Домашнее задание
- воспитание правильной самооценки;
- создание ситуации “успеха” для каждого ученика.
п.44, знать определение, элементы трапеции, ее виды, знать свойства трапеции, уметь их доказывать, №388, №390.
V. Итог урока. В конце урока даётся ребятам анкета, которая позволяет осуществить самоанализ, дать качественную и количественную оценку уроку.
\[{\Large{\text{Произвольная трапеция}}}\]
Определения
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами.
Высота трапеции – это перпендикуляр, опущенный из любой точки одного основания к другому основанию.
Теоремы: свойства трапеции
1) Сумма углов при боковой стороне равна \(180^\circ\) .
2) Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.
Доказательство
1) Т.к. \(AD\parallel BC\) , то углы \(\angle BAD\) и \(\angle ABC\) – односторонние при этих прямых и секущей \(AB\) , следовательно, \(\angle BAD +\angle ABC=180^\circ\) .
2) Т.к. \(AD\parallel BC\)
и \(BD\)
– секущая, то \(\angle DBC=\angle
BDA\)
как накрест лежащие.
Также \(\angle BOC=\angle AOD\)
как вертикальные.
Следовательно, по двум углам \(\triangle BOC \sim \triangle AOD\)
.
Докажем, что \(S_{\triangle AOB}=S_{\triangle COD}\) . Пусть \(h\) – высота трапеции. Тогда \(S_{\triangle ABD}=\frac12\cdot h\cdot AD=S_{\triangle ACD}\) . Тогда: \
Определение
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство*
1) Докажем параллельность.

Проведем через точку \(M\) прямую \(MN"\parallel AD\) (\(N"\in CD\) ). Тогда по теореме Фалеса (т.к. \(MN"\parallel AD\parallel BC, AM=MB\) ) точка \(N"\) - середина отрезка \(CD\) . Значит, точки \(N\) и \(N"\) совпадут.
2) Докажем формулу.
Проведем \(BB"\perp AD, CC"\perp AD\) . Пусть \(BB"\cap MN=M", CC"\cap MN=N"\) .

Тогда по теореме Фалеса \(M"\) и \(N"\) - середины отрезков \(BB"\) и \(CC"\) соответственно. Значит, \(MM"\) – средняя линия \(\triangle ABB"\) , \(NN"\) - средняя линия \(\triangle DCC"\) . Поэтому: \
Т.к. \(MN\parallel AD\parallel BC\) и \(BB", CC"\perp AD\) , то \(B"M"N"C"\) и \(BM"N"C\) – прямоугольники. По теореме Фалеса из \(MN\parallel AD\) и \(AM=MB\) следует, что \(B"M"=M"B\) . Значит, \(B"M"N"C"\) и \(BM"N"C\) – равные прямоугольники, следовательно, \(M"N"=B"C"=BC\) .
Таким образом:
\ \[=\dfrac12 \left(AB"+B"C"+BC+C"D\right)=\dfrac12\left(AD+BC\right)\]
Теорема: свойство произвольной трапеции
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.

Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем, что точки \(P\) , \(N\) и \(M\) лежат на одной прямой.

Проведем прямую \(PN\) (\(P\) – точка пересечения продолжений боковых сторон, \(N\) – середина \(BC\) ). Пусть она пересечет сторону \(AD\) в точке \(M\) . Докажем, что \(M\) – середина \(AD\) .
Рассмотрим \(\triangle BPN\) и \(\triangle APM\) . Они подобны по двум углам (\(\angle APM\) – общий, \(\angle PAM=\angle PBN\) как соответственные при \(AD\parallel BC\) и \(AB\) секущей). Значит: \[\dfrac{BN}{AM}=\dfrac{PN}{PM}\]
Рассмотрим \(\triangle CPN\) и \(\triangle DPM\) . Они подобны по двум углам (\(\angle DPM\) – общий, \(\angle PDM=\angle PCN\) как соответственные при \(AD\parallel BC\) и \(CD\) секущей). Значит: \[\dfrac{CN}{DM}=\dfrac{PN}{PM}\]
Отсюда \(\dfrac{BN}{AM}=\dfrac{CN}{DM}\) . Но \(BN=NC\) , следовательно, \(AM=DM\) .
2) Докажем, что точки \(N, O, M\) лежат на одной прямой.

Пусть \(N\) – середина \(BC\) , \(O\) – точка пересечения диагоналей. Проведем прямую \(NO\) , она пересечет сторону \(AD\) в точке \(M\) . Докажем, что \(M\) – середина \(AD\) .
\(\triangle BNO\sim \triangle DMO\) по двум углам (\(\angle OBN=\angle ODM\) как накрест лежащие при \(BC\parallel AD\) и \(BD\) секущей; \(\angle BON=\angle DOM\) как вертикальные). Значит: \[\dfrac{BN}{MD}=\dfrac{ON}{OM}\]
Аналогично \(\triangle CON\sim \triangle AOM\) . Значит: \[\dfrac{CN}{MA}=\dfrac{ON}{OM}\]
Отсюда \(\dfrac{BN}{MD}=\dfrac{CN}{MA}\) . Но \(BN=CN\) , следовательно, \(AM=MD\) .
\[{\Large{\text{Равнобедренная трапеция}}}\]
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
1) Рассмотрим равнобедренную трапецию \(ABCD\) .

Из вершин \(B\) и \(C\) опустим на сторону \(AD\) перпендикуляры \(BM\) и \(CN\) соответственно. Так как \(BM\perp AD\) и \(CN\perp AD\) , то \(BM\parallel CN\) ; \(AD\parallel BC\) , тогда \(MBCN\) – параллелограмм, следовательно, \(BM = CN\) .
Рассмотрим прямоугольные треугольники \(ABM\) и \(CDN\) . Так как у них равны гипотенузы и катет \(BM\) равен катету \(CN\) , то эти треугольники равны, следовательно, \(\angle DAB = \angle CDA\) .
2) 
Т.к. \(AB=CD, \angle A=\angle D, AD\) – общая, то по первому признаку . Следовательно, \(AC=BD\) .
3) Т.к. \(\triangle ABD=\triangle ACD\) , то \(\angle BDA=\angle CAD\) . Следовательно, треугольник \(\triangle AOD\) – равнобедренный. Аналогично доказывается, что и \(\triangle BOC\) – равнобедренный.
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
Рассмотрим трапецию \(ABCD\) , такую что \(\angle A = \angle D\) .

Достроим трапецию до треугольника \(AED\) как показано на рисунке. Так как \(\angle 1 = \angle 2\) , то треугольник \(AED\) равнобедренный и \(AE = ED\) . Углы \(1\) и \(3\) равны как соответственные при параллельных прямых \(AD\) и \(BC\) и секущей \(AB\) . Аналогично равны углы \(2\) и \(4\) , но \(\angle 1 = \angle 2\) , тогда \(\angle 3 = \angle 1 = \angle 2 = \angle 4\) , следовательно, треугольник \(BEC\) тоже равнобедренный и \(BE = EC\) .
В итоге \(AB = AE - BE = DE - CE = CD\) , то есть \(AB = CD\) , что и требовалось доказать.
2) Пусть \(AC=BD\) . Т.к. \(\triangle AOD\sim \triangle BOC\) , то обозначим их коэффициент подобия за \(k\) . Тогда если \(BO=x\) , то \(OD=kx\) . Аналогично \(CO=y \Rightarrow AO=ky\) .

Т.к. \(AC=BD\) , то \(x+kx=y+ky \Rightarrow x=y\) . Значит \(\triangle AOD\) – равнобедренный и \(\angle OAD=\angle ODA\) .
Таким образом, по первому признаку \(\triangle ABD=\triangle ACD\) (\(AC=BD, \angle OAD=\angle ODA, AD\) – общая). Значит, \(AB=CD\) , чтд.
Тема урока
Трапеция
Цели урока
Продолжать знакомить с новыми определениями в геометрии;
Закрепить знания об уже изученных геометрических фигурах;
Познакомить с формулировкой и доказательствами свойств трапеции;
Обучить применению свойств различных фигур при решении задач и выполнении заданий;
Продолжать развивать у школьников внимание, логическое мышление и математическую речь;
Воспитывать интерес к предмету.
Задачи урока
Вызвать интерес к знаниям по геометрии;
Продолжать упражнять школьников в решении задач;
Вызвать познавательный интерес к урокам математики.
План урока
1. Повторить материал, изученный ранее.
2. Знакомство с трапецией, ее свойствами и признаками.
3. Решение задач и выполнение заданий.
Повторение ранее изученного материала
На предыдущем уроке вы знакомились с такой фигурой, как четырехугольник. Давайте закрепим пройденный материал и ответим на поставленные вопросы:
1. Сколько углов и сторон имеет 4-х угольник?
2. Сформулируйте определение 4-х угольника?
3. Какое название носят противоположные стороны 4-х угольника?
4. Какие виды четырехугольников вам известны? Перечислите их и дайте определение каждого из них.
5. Изобразите пример выпуклого и невыпуклого четырехугольника.
Трапеция. Общие свойства и определение
Трапеция - это такая четырехугольная фигура, у которой только одна пара противолежащих сторон параллельна.
В геометрическом определении к трапеции относится такой 4-х угольник, который имеет две параллельные стороны, а две другие – нет.
Название такой необычной фигуры, как «трапеция» произошло от слова «трапезион», что в переводе с греческого языка, обозначает слово «столик», от которого произошли также слово «трапеза» и другие родственные слова.
В некоторых случаях в трапеции пара противоположных сторон параллельна, а другая его пара не является параллельной. В таком случае трапеция носит название криволинейной.
Элементы трапеции

Трапеция состоит из таких элементов, как основание, боковые линии, средняя линия и ее высота.
Основанием трапеции называют ее параллельные стороны;
Боковыми сторонами называют две другие стороны трапеции, которые не есть параллельными;
Средней линией трапеции называют отрезок, который соединяет середины его боковых сторон;
Высотой трапеции считается расстояние между ее основаниями.
Виды трапеций

Задание:
1. Сформулируйте определение равнобедренной трапеции.
2. Какая трапеция называется прямоугольной?
3. Что значит остроугольная трапеция?
4. Какая трапеция относится к тупоугольной?
Общие свойства трапеции
Во-первых, средняя линия трапеции находится параллельно основанию фигуры и равняется ее полусумме;
Во-вторых, отрезок, который соединяет середины диагоналей 4-х угольной фигуры, равняется полуразности ее оснований;
В-третьих, в трапеции параллельно лежащие прямые, которые пересекают стороны угла данной фигуры, отсекают пропорциональные отрезки от сторон угла.
В-четвертых, в любого из видов трапеции сумма углов, которые прилегают к ее боковой стороне, равны 180°.
Где еще присутствует трапеция
Слово «трапеция» присутствует не только в геометрии, она имеет более широкое применение в повседневной жизни.
Это необычное слово мы можем встретить, просматривая спортивные соревнования гимнастов, выполняющих акробатические упражнения на трапеции. В гимнастике трапецией называют спортивный снаряд, который состоит из перекладины, подвешенной на двух веревках.
Также это слово можно услышать, занимаясь в спортивном зале или в среде людей, которые занимаются бодибилдингом, так как трапеции - это не только геометрическая фигура или спортивный акробатический снаряд, но и мощные мышцы спины, которые расположены сзади за шеей.

На рисунке изображена воздушная трапеция, которую изобрел для цирковых акробатов артист Джулиус Леотард еще в девятнадцатом веке во Франции. Вначале создатель этого номера устанавливал свой снаряд на небольшой высоте, но в итоге он был перенесен под самый купол цирка.
Воздушные гимнасты в цирке выполняют трюки перелетов из трапеции на трапецию, исполняют перекрёстные полёты, проделывают в воздухе сальто-мортале.
В конном виде спорта, трапецией называют упражнение для растяжки или потягивание тела лошади, которое очень полезно и приятно для животного. Во время стойки лошади в положении трапеции работает растяжка ног животного или мышц его спины. Это красивое упражнение мы можем наблюдать во время поклона или так называемого «переднего кранча», когда лошадь глубоко прогибается.
Задание: Наведите свои примеры о том, где еще в повседневной жизни можно услышать слова «трапеция»?
А известно ли вам, что впервые в 1947 году известный французский модельер Кристиан Диор произвел показ мод, в котором присутствовал силуэт юбки-трапеции. И хотя уже прошло более шестидесяти лет, этот силуэт до сих пор в моде, и не теряет своей актуальности, и по сей день.

В гардеробе английской королевы юбка-трапеция стала непременным предметом и ее визитной карточкой.
Напоминающая геометрическую форму трапеции, юбка с одноименным названием прекрасно сочетается с любыми кофточками, блузами, топами и пиджаками. Классичность и демократичность этого популярного фасона позволяет ее носить и со строгими пиджаками и немного легкомысленными топами. В такой юбке будет уместно появляться как в офисе, так и на дискотеке.
Задачи с трапецией
Для облегчения решения задач с трапециями важно помнить несколько основных правил:
Во-первых, проведите две высоты: ВF и СК.
В одном из случаев, в результате вы получите прямоугольник – ВСFК из чего понятно, что FК=ВС.
АD=АF+FК+КD, отсюда АD=АF+ВС+КD.
К тому же сразу очевидно, что АВF и DСК – это прямоугольные треугольники.

Возможен еще такой вариант, когда трапеция не совсем стандартная, где
АD=АF+FD=АF+FК–DК=АF+ВС–DК.

Но самый простой вариант, если наша трапеция – равнобедренная. Тогда решать задачу становиться еще легче, потому что АВF и DСК – это прямоугольные треугольники, и они равны. АВ=СD, так как трапеция равнобедренная, а ВF=СК, как высоты трапеции. Из равенства треугольников следует равенство соответствующих сторон.
Описанная окружность и трапеция. Здравствуйте! Для вас ещё одна публикация, в которой рассмотрим задачи с трапециями. Задания входят в состав экзамена по математике. Здесь они объединены в группу, дана не просто одна трапеция, а комбинация тел – трапеция и окружность. Большинство из таких задачек решаются устно. Но есть и такие на которые нужно обратить особое внимание, например, задача 27926.
Какую теорию необходимо помнить? Это:
Задачи с трапециями, которые имеются на блоге можно посмотреть здесь .
27924. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.

Отметим, что описать окружность можно только около равнобедренной трапеции. Нам дана средняя линия, значит можем определить сумму оснований, то есть:
Значит сумма боковых сторон будет равна 22–10=12 (периметр минус основания). Так как боковые стороны равнобедренной трапеции равны, то одна сторона будет равна шести.
27925. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60 0 , большее основание равно 12. Найдите радиус описанной окружности этой трапеции.

Если вы решали задачи с окружностью и вписанным в неё шестиугольником, то сразу озвучите ответ – радиус равен 6. Почему?
Посмотрите: равнобедренная трапеция с углом при основании равным 60 0 и равными сторонами AD, DC и CB, представляет собой половину правильного шестиугольника:

В таком шестиугольнике отрезок соединяющий противоположные вершины проходит через центр окружности. *Центр шестиугольника и центр окружности совпадают, подробнее
То есть большее основание этой трапеции совпадает с диаметром описанной окружности. Таким образом радиус равен шести.
*Конечно, можно рассмотреть равенство треугольников ADO, DOС и OCB. Доказать что они равносторонние. Далее сделать вывод о том, что угол AOB равен 180 0 и точка О равноудалена от вершин A, D, C и B, а и значит АО=ОВ=12/2=6.
27926. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.

Отметим, что центр описанной окружности лежит на оси симметрии, при чём если построить высоту трапеции проходящую через этот центр, то она при пересечении с основаниями разделит их пополам. Покажем это на эскизе, также соединим центр с вершинами:

Отрезок EF является высотой трапеции, его нам нужно найти.
В прямоугольном треугольнике OFC нам известна гипотенуза (это радиус окружности), FC=3 (так как DF=FC). По теореме Пифагора можем вычислить OF:

В прямоугольном треугольнике OEB нам известна гипотенуза (это радиус окружности), EB=4 (так как AE=EB). По теореме Пифагора можем вычислить OE:

Таким образом EF=FO+OE=4+3=7.
Теперь важный нюанс!
В этой задаче на рисунке чётко показано, что основания лежат по разные стороны от центра окружности, поэтому задача решается именно так.
А если бы в условии не было дано эскиза?
Тогда у задачи было бы два ответа. Почему? Посмотрите внимательно – в любую окружность можно вписать две трапеции с заданными основаниями:
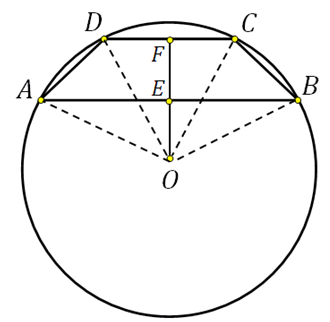
*То есть при данных основаниях трапеции и радиусе окружности существует две трапеции.
И решение будет «второго варианта» будет следующим.
По теореме Пифагора вычисляем OF:
Также вычислим OE:

Таким образом EF=FO–OE=4–3=1.
Конечно, в задаче с кратким ответом на ЕГЭ двух ответов быть не может, и подобная задача без эскиза дана не будет. Поэтому обратите особое внимание на эскиз! А именно: как расположены основания трапеции. А вот в заданиях с развёрнутым ответом такая в прошлые годы присутствовала (немного с усложнённым условием). Тот, кто рассматривал только один вариант расположения трапеции теряли балл на этом задании.
27937. Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.

Здесь сразу следует вспомнить свойство четырёхугольника описанного около окружности:
Суммы противоположных сторон любого четырёхугольника описанного около окружности равны.
С такой формой как трапеция, мы встречаемся в жизни довольно часто. К примеру, любой мост который выполнен из бетонных блоков, является ярким примером. Более наглядным вариантом можно считать рулевое управление каждого транспортного средства и прочее. О свойствах фигуры было известно еще в Древней Греции
, которую более детально описал Аристотель в своем научном труде «Начала». И знания, выведенные тысячи лет назад актуальны и по сегодня. Поэтому ознакомимся с ними более детально.
Основные понятия
Рисунок 1. Классическая форма трапеции.
Трапеция по своей сути является четырехугольником, состоящим из двух отрезков которые параллельны, и двух других, которые не параллельны. Говоря об этой фигуре всегда необходимо помнить о таких понятиях как: основания, высота и средняя линия. Два отрезка четырехугольника которые друг другу называются основаниями (отрезки AD и BC). Высотой называют отрезок перпендикулярный каждому из оснований (EH), т.е. пересекаются под углом 90° (как это показано на рис.1).
 Если сложить все градусные меры внутренних , то сумма углов трапеции будет равна 2π (360°), как и у любого четырехугольника. Отрезок, концы которого являются серединами боковин (IF) именуют средней линей.
Длина этого отрезка составляет сумму оснований BC и AD деленную на 2.
Если сложить все градусные меры внутренних , то сумма углов трапеции будет равна 2π (360°), как и у любого четырехугольника. Отрезок, концы которого являются серединами боковин (IF) именуют средней линей.
Длина этого отрезка составляет сумму оснований BC и AD деленную на 2.
Существует три вида геометрической фигуры: прямая, обычная и равнобокая. Если хоть один угол при вершинах основания будет прямой (например, если ABD=90°), то такой четырехугольник называют прямой трапецией. Если боковые отрезки равны (AB и CD), то она называется равнобедренной (соответственно углы при основаниях равны).
Как найти площадь
Для того, чтобы найти площадь четырехугольника ABCD пользуются следующей формулой:

Рисунок 2. Решение задачи на поиск площади
Для более наглядного примера решим легкую задачу. К примеру, пускай верхнее и нижнее основания равны по 16 и 44 см соответственно, а боковые стороны – 17 и 25 см. Построим перпендикулярный отрезок из вершины D таким образом, чтобы DE II BC (как это изображено на рисунке 2). Отсюда получаем, что
Пускай DF – будет . Из ΔADE (который будет равнобоким), получим следующее:
Т.е., выражаясь простым языком, мы вначале нашли высоту ΔADE, которая по совместительству является и высотой трапеции. Отсюда вычислим по уже известной формуле площадь четырехугольника ABCD, с уже известным значением высоты DF.
Отсюда, искомая площадь ABCD равна 450 см³. То есть можно с уверенностью сказать, что для того, чтобы вычислить площадь трапеции потребуется только сумма оснований и длина высоты.
Важно! При решении задача не обязательно найти значение длин по отдельности, вполне допускается, если будут применены и другие параметры фигуры, которые при соответствующем доказательстве будут равны сумме оснований.
Виды трапеций
В зависимости от того, какие стороны имеет фигура, какие углы образованы при основаниях, выделяют три вида четырехугольника: прямоугольная, разнобокая и равнобокая.
Разнобокая
Существует две формы: остроугольная и тупоугольная . ABCD остроугольна только в том случае, когда углы при основании (AD) острые, а длины сторон разные. Если величина одного угла число Пи/2 более (градусная мера более 90°), то получим тупоугольную.
Если боковины по длине равны
Рисунок 3. Вид равнобокой трапеции
Если непараллельные стороны равны по длине, тогда ABCD называется равнобокой (правильной). При этом у такого четырехугольника градусная мера углов при основании одинакова, их угол будет всегда меньше прямого. Именно по этой причине равнобедренная никогда не делится на остроугольные и тупоугольные. Четырехугольник такой формы имеет свои специфические отличия, к числу которых относят:
- Отрезки соединяющие противоположные вершины равны.
- Острые углы при большем основании составляют 45° (наглядный пример на рисунке 3).
- Если сложить градусные меры противоположных углов, то в сумме они будут давать 180°.
- Вокруг любой правильной трапеции можно построить .
- Если сложить градусную меру противоположных углов, то она равна π.
Более того, в силу своего геометрического расположения точек существуют основные свойства равнобедренной трапеции :
Значение угла при основании 90°
Перпендикулярность боковой стороны основания — емкая характеристика понятия «прямоугольная трапеция». Двух боковых сторон с углами при основании быть не может, потому как в противном случае это будет уже прямоугольник. В четырехугольниках такого типа вторая боковая сторона всегда будет образовывать острый угол с большим основанием, а с меньшим — тупой. При этом, перпендикулярная сторона также будет являться и высотой.
Отрезок между серединами боковин
Если соединить середины боковых сторон, и полученный отрезок будет параллельный основаниям, и равен по длине половине их суммы, то образованная прямая будет средней линией. Значение этого расстояния вычисляется по формуле:
Для более наглядного примера рассмотрим задачу с применением средней линии.
Задача. Средняя линия трапеции равна 7 см, известно, что одна из сторон больше другой на 4 см (рис.4). Найти длины оснований.
Рисунок 4. Решение задачи на поиск длин оснований
Решение. Пусть меньшее основание DC будет равно x см, тогда большее основание будет равняться соответственно (x+4) см. Отсюда, используя формулу средней линии трапеции получим:
Получается, что меньшее основание DC равно 5 см, а большее равняется 9 см.
Важно! Понятие средней линии является ключевым при решении многих задач по геометрии. На основании её определения, строятся многие доказательства для других фигур. Используя понятие на практике, возможно более рациональное решение и поиск необходимой величины.
Определение высоты, и способы как её найти
Как уже отмечалось ранее, высота представляет собой отрезок, который пересекает основания под углом 2Пи/4 и является кратчайшим расстоянием между ними. Перед тем как найти высоту трапеции, следует определиться какие даны входные значения. Для лучшего понимания рассмотрим задачу. Найти высоту трапеции при условии, что основания равны 8 и 28 см, боковые стороны 12 и 16 см соответственно.
Рисунок 5. Решение задачи на поиск высоты трапеции
Проведем отрезки DF и CH под прямыми углами к основанию AD.Согласно определению, каждый из них будет являться высотой заданной трапеции (рис.5). В таком случае, зная длину каждой боковины, при помощи теоремы Пифагора, найдем чему равна высота в треугольниках AFD и BHC.
Сумма отрезков AF и HB равна разности оснований, т.е.:
Пускай длина AF будет равняться x cм, тогда длина отрезка HB= (20 – x)см. Как было установлено, DF=CH , отсюда .
Тогда получим следующее уравнение:
Получается, что отрезок AF в треугольнике AFD равен 7,2 см, отсюда вычислим по той же теореме Пифагора высоту трапеции DF:
Т.е. высота трапеции ADCB будет равна 9,6 см. Как можно убедиться, что вычисление высоты — процесс больше механический, и основывается на вычислениях сторон и углов треугольников. Но, в ряде задач по геометрии, могут быть известны только градусы углов, в таком случае вычисления будут производиться через соотношение сторон внутренних треугольников.
Важно! В сущности трапецию часто рассматривают как два треугольника, или как комбинацию прямоугольника и треугольника. Для решения 90% всех задач, встречаемых в школьных учебниках, свойства и признаки этих фигур. Большинство формул, для этого ГМТ, выведены полагаясь на «механизмы» для указанных двух типов фигур.
Как быстро вычислить длину основания
Перед тем, как найти основание трапеции необходимо определить какие параметры уже даны, и как их рационально использовать. Практическим подходом является извлечение длины неизвестного основания из формулы средней линии. Для более ясного восприятия картинки покажем на примере задачи, как это можно сделать. Пускай известно, что средняя линия трапеции составляет 7 см, а одно из оснований 10 см. Найти длину второй основы.
Решение: Зная, что средняя линия равна половине суммы основ, можно утверждать, что их сумма равна 14 см.
(14 см = 7 см × 2). Из условия задачи, мы знаем, что одно из равно 10 см, отсюда меньшая сторона трапеции будет равна 4 см (4 см = 14 – 10).
Более того, для более комфортного решения задач подобного плана, рекомендуем хорошо выучить такие формулы из области трапеции как :
- средняя линия;
- площадь;
- высота;
- диагонали.
Зная суть (именно суть) этих вычислений можно без особого труда узнать искомое значение.
Видео: трапеция и ее свойства
Видео: особенности трапеции
Вывод
Из рассмотренных примеров задач можно сделать нехитрый вывод, что трапеция, в плане вычисления задач, является одной из простейших фигур геометрии. Для успешного решения задач прежде всего не стоит определиться с тем, какая информация известна об описываем объекте, в каких формулах их можно применить, и определиться с тем, что требуется найти. Выполняя этот простой алгоритм, ни одна задача с применением этой геометрической фигуры не составит усилий.





